We’ve now seen the guts of a codebase that does Excel calculations. On it’s own it isn’t too revealing to look at algorithms and functions, so I thought it wise to show some of the tests that I wrote.
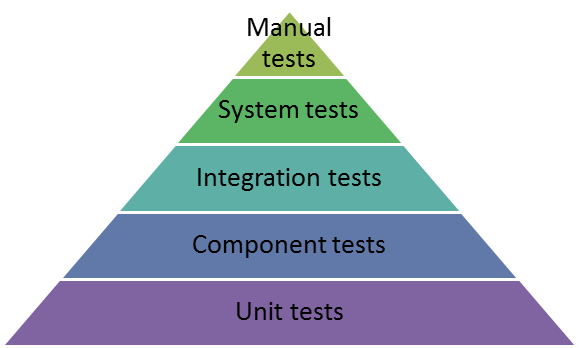
I’ll start by referencing the Test Pyramid:
The long and short of it is that we want to write more Unit tests than Component tests, more Component tests than Integration tests, and so on.
The Test Pyramid and Functional Programming
I’ve found functional programming to fit quite nicely into this paradigm — its emphasis on composition and pipelining means that a Component is quite often made up of a handful of composed Units, with multiple Components integrated together by composition once more. By testing each unit, we then feel sufficiently comfortable that we almost only need to smoke-test the component.
That is, if we have something like
let function1 = ...
let function2 = ...
let function3 = ...
let composite = function1 >> function2 >> function 3
and we thoroughly test function1, function2 and function3, we barely need to test composite. Granted, this security is partly due to the fantastic compile-time type system that F# gives us — the mere fact that the code above compiles is a reasonably strong indicator that the behaviour of composite is correct!
Having seen how good functional architecture leads us naturally on to good testing practices, let’s talk about the available testing tools in F#.
NUnit, NCrunch, and Unquote
Fans of C# might look at the above and think: well I know what the first two are, they are a formidable combination for continuous testing in Visual Studio, but how do they work in F#, and what is Unquote?
Taking a step back, if you are a .NET developer and don’t use NCrunch, start using it now!! Even if you aren’t doing Test-Driven Development, it will give you the confidence to know which bits of your code are tested, which aren’t, and whether your last one-line chance has broken anything. In terms of F# support, well, it just works like it does with C#!
The new boy on the block, Unquote, is pretty cool too. It uses two really nice features of F# that we haven’t looked a much yet, Code Quotations and Custom Operators. The resulting test syntax is beautiful and very readable — more that can be said about things like NUnit Assertions.
The easiest way to see it in action (other than trying it yourself) is to look at some real tests. Casting your mind back to the first bits of code we looked at last time, we had this function called StringToTokenList that took the contents of an Excel formula and turned it into a list of Token items that were strongly typed.
Here’s the first test for that function:
[<Test>]
let ``StringToTokenList 1+2``() =
StringToTokenList "1+2" =! [ Val(float 1)
Operator Operator.Add
Val(float 2) ]
A couple of nice things here are that:
- We don’t have to bother with the tedious Arrange/Act/Assert pattern that pervades object-oriented tests. We simply write what we want to be taken as true, and use Unquote’s equality operator
=!. - We can name the tests with as much verbosity as required, thanks to F#’s double-backtick notation. I’m not sure I am using this to full potential yet — maybe I’m stuck in the C# way of terse test names!
- In this simple example I didn’t use a code quotation, but if the test setup were more complex I could do that rather than use a custom equality operator.
- It’s a minor thing, but being able to initialise arrays using separate lines and no semi-colons is handy.
It carries on and gets more complicated — we can include whitespace, brackets, references, etc. in the expression, but the tests look exactly the same:
[<Test>]
let ``StringToTokenList multi digit integers``() =
StringToTokenList "( 123 + 321 )" =! [ LeftBracket
Val(float 123)
Operator Operator.Add
Val(float 321)
RightBracket ]
[<Test>]
let ``StringToTokenList A1 + A2 * BB312``() =
StringToTokenList "A1 + A2 * BB312" =! [ Ref { col = 1
row = 1 }
Operator Operator.Add
Ref { col = 1
row = 2 }
Operator Operator.Multiply
Ref { col = 54
row = 312 } ]
I’ve introduced you to the tools and frameworks I’ll use for testing, and hopefully you have some idea of what a Token list looks like, so let’s look at some more of the code tests before we move on to the working system!
Testing the Operators, Parser, and Calculator
I said last time that I had made the operators work on lists as well as numbers, and that it would be easy to extend this functionality to other types.
To test the Shunting-Yard algorithm, I was slightly naughty and used the example on the Wikipedia page. Here’s what my test looked like:
[<Test>]
let ``InfixToPostfix 5 + ((1 + 2) * 4) - 3``() =
InfixToPostfix [ Val (float 5)
Operator Operator.Add
LeftBracket
LeftBracket
Val (float 1)
Operator Operator.Add
Val (float 2)
RightBracket
Operator Operator.Multiply
Val (float 4)
RightBracket
Operator Operator.Subtract
Val (float 3) ]
=! PostFixList([ Val (float 5)
Val (float 1)
Val (float 2)
Operator Operator.Add
Val (float 4)
Operator Operator.Multiply
Operator Operator.Add
Val (float 3)
Operator Operator.Subtract ])
Believe it or not, this one test managed to root out enough issue with my original implementation of the algorithm that all the subsequent tests passed first time — I guess that’s why it’s on the Wikipedia page!
For the raw operator functions such as add, I briefly experiemented with Property-Based Testing, but to be honest I struggled to grasp the nuances straight away. The code for those tests is here, and whislt it works for things like addition for which we have a good understanding of the required properties, I couldn’t easily translate it to higher-level concepts such as operator precedence.
The ‘normal’ tests I wrote were pretty basic, e.g.
[<Test>]
let ``Add x y works on values``() = Add (Val 1.0) (Val 2.0) =! Val 3.0
The calculator tests were slightly more interesting (but not much). Taking the previous example used to test the Shunting-Yard algorithm, we have
[<Test>]
let ``Calculate 5 + ((1 + 2) * 4) - 3 = 14``() =
Calculate(PostFixList([ Val(float 5)
Val(float 1)
Val(float 2)
Operator Operator.Add
Val(float 4)
Operator Operator.Multiply
Operator Operator.Add
Val(float 3)
Operator Operator.Subtract ]))
=! ValResult(float 14)
Pretty basic tests — the idea of showing you some of them was to give a more intuitive feel of what the output code looked like.
System Tests: using the functions in Excel!
The screenshot above shows a few examples of our calculator replicating Excel functionality, which serves to show that it does roughly what it should! The bottom example shows a vector calculation
This next shot shows something a bit more complex. If you look at the formula bar, you will see that it’s doing more than just arithmetic with numbers. It’s taking a reference to a cell containing 10,000 Monte Carlo simulations, performing a calculation on them to account for changes in exchange rates, and saving the results (10,000 new simulations) in a single cell.
Whilst this is very much a prototype, I think it’s a long way towards solving the problem that I originally wanted to solve. Sure, it needs a bit more TLC to be race-ready, but I think I’ve learned a decent amount about both Excel and F# in the process!
Next Time
Something a little different from the usual. I’ll be talking about the SOLID prinicples of object-oriented design and how they are much more compatible with functional programming that first meets the eye.


No comments:
Post a Comment